Math/선형대수
선형대수 : 8. 전치(transpose)
bright jazz music
2022. 7. 27. 08:34
전치
- 전치는 행과 열을 바꾸는 것이다. 전치행렬은 행과 열을 교환하여 얻는 행렬이다.
- 행렬 A의 전치는 아래와 같이 표현한다.
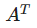
전치의 예
| LaTeX | 수식 |
| $ \begin{align} A &=\begin{pmatrix} 1 & 2& 3\\ 4 & 5 & 6 \end{pmatrix} \\ \\ A^T &= \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} \end{align}$ |
 |
| $ \begin{align} B &=\begin{pmatrix} a & b\\ c & d \\ e & f\end{pmatrix} \\ \\ B^T &= \begin{pmatrix} a & c & e\\ b & d & f \end{pmatrix} \end{align}$ |
 |
파이썬에서의 전치의 구현
- NumPy에서는 행렬을 나타내는 배열명 뒤에 .T를 붙이면 전치된다.
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6]]) #행렬
print(a.T) # 전치
# [[1 4]
# [2 5]
# [3 6]]
행렬곱과 전치
- 행렬곱(일반적인 행렬의 곱)을 하기 위해서는 앞의 행렬의 열 수와 뒤 행렬의 행 수가 일치해야 한다.
- 앞의 행렬의 열 수와 뒤 행렬의 행 수가 일치하지 않는 경우가 있다.
- 이 경우, 행렬을 전치하여 일치시킬 수 있으면 전치하여 행렬곱을 구한다.
아래의 예를 참고하자.
- A는 lxn의 행렬이다.
- B는 mxn의 행렬이다.
- 이 때 n과 m이 일치하지 않으면 행렬곱을 할 수 없다.

- 따라서 전치가 가능한지 고려한다.
- 전치가 가능하여 열과 행을 일치시킬 수 있는 경우 아래와 같이 행렬곱을 할 수 있다.

전치와 행렬곱 구현
import numpy as np
a = np.array([[0, 1, 2],
[1, 2, 3]]) #2x3행렬
b = np.array([[0, 1, 2],
[1, 2, 3]]) #2x3행렬. #앞 행렬의 열과 뒤 행렬의 행 수가 일치하지 않음.
#행렬곱 불가
#print(np.dot(a, b)) 행렬곱을 시도할 경우 아래와 같은 에러 발생
#ValueError: shapes (2,3) and (2,3) not aligned: 3 (dim 1) != 2 (dim 0)
print(np.dot(a, b.T)) #b행렬을 전치하여 행렬곱 수행
#[[ 5 8]
# [ 8 14]]
실습
#a행렬 또는 b행렬을 전치하고 a와 b의 행렬곱을 구하라
import numpy as np
a = np.array([[0, 1, 2],
[1, 2, 3]])
b = np.array([[0, 1, 2],
[2, 3, 4]])
print(np.dot(a.T, b)) #a행렬을 전치하여 행렬곱 수행
print()
print(np.dot(a, b.T)) #a행렬을 전치하여 행렬곱 수행
# [[ 2 3 4]
# [ 4 7 10]
# [ 6 11 16]]
#
# [[ 5 11]
# [ 8 20]]
둘 중에 어떤 것을 어떤 이유로 사용해야 하는가?
참고:
https://ko.wikipedia.org/wiki/%EC%A0%84%EC%B9%98%ED%96%89%EB%A0%AC