미분 : 1. 극한과 미분(극한, 도함수, 미분, 상미분)

Math/미적분

bright jazz music 2022. 10. 4. 13:00

#극한과 미분
#극한은 함수에서 변수값을 어떤 값에 가깝게 할 때 함수의 값이 한없이 가까워지는 값을 말한다.

#y=x^2 + 1 에서 x가 점점 작아지는 경우 0에 수렴한다.
#따라서 y=1에 가까워진다.

#미분은 변화의 비율을 말한다.

LaTeX	수식
$lim_{x \to 0}{y} = lim_{x \to 0}{(x^2+1)}=1 $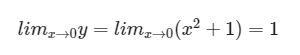

이 식의 의미 : "x를 한없이 0에 가깝게 하면 y가 1에 가까워진다."

함수 y=f(x)에서, x의 미소한 변화량을 x로 하면, x를 Δx 만큼 변화 시킬 때의 y 값은 아래와 같다.

LaTeX	수식
$y=f(x+\Delta{x})$ *델타의 기호가 대문자임을 주의. d를 쓸 경우 소문자 델타로 표기됨

이 때 y의 미소한 변화량은 다음과 같다.

LaTeX	수식
$\Delta{y}= f(x+\Delta{x})-f(x)$

따라서 y의 미소한 변화 Δy와 x의 미소한 변화 Δx의 비율은 다음 식으로 표현한다.

LaTeX	수식
$\frac{\Delta{y}}{\Delta{x}} = \frac{f(x+\Delta{x}) -f(x)}{\Delta{x}}$

이 식에서 Δx의 값이 0에 한없이 가까워지는 극한을 생각하자.

이 극한은 새로운 함수 f '(x)로서 나타낼 수 있다.

LaTeX	수식
$f\prime(x) = lim_{\Delta{x} \to 0}{\frac{f(x+\Delta{x}) -f(x)}{\Delta{x}}}$

여기서 '도(導)'는 유도하다, 이끌다의 뜻을 가진 한자이다. derivative는 파생되었다는 뜻을 가지고 있다. 따라서 도함수는 원래 함수에서 유도되어 떨어져 나온 함수라는 뜻을 가지고 있다고 할 수 있다.

함수 f(x)를 미분하라 == 함수 f(x)의 도함수 f '(x)를 구하라 == x의 변화에 대한 y의 변화의 비율을 구하라

도함수는 아래와 같이 표기할 수 도 있다.

LaTeX	수식
$f\prime(x) = \frac{df(x)}{dx}=\frac{d}{dx}f(x)$

여기의 예시에서는 함수의 변수가 x 하나뿐이었다. 이와 같은 1변수 함수의 대한 미분을 상미분이라고 한다.

x에 대한 y의 변화 비율을 기울기(경사, 그라디언트, 구배)라고 부르는데, 도함수를 사용하여 1변수 함수 상의 특정 점에서의 기울기를 구할 수 있다. 함수 f(x) 상의 어떤 점 (a, f(a))에서의 기울기는 f '(a)가 된다.

아래 그림 참고

ㅇ