| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 자료구조와 함께 배우는 알고리즘 입문
- 스프링 시큐리티
- 선형대수
- d
- 자료구조와함께배우는알고리즘입문
- 처음 만나는 AI 수학 with Python
- network configuration
- 티스토리 쿠키 삭제
- 자바편
- 처음 만나는 AI수학 with Python
- 알파회계
- resttemplate
- 네트워크 설정
- 서버설정
- baeldung
- /etc/network/interfaces
- 코드로배우는스프링웹프로젝트
- iterator
- ㅒ
- 친절한SQL튜닝
- 구멍가게코딩단
- 코드로배우는스프링부트웹프로젝트
- 데비안
- 목록처리
- 이터레이터
- GIT
- 페이징
- 리눅스
- Kernighan의 C언어 프로그래밍
- 스프링부트핵심가이드
- Today
- Total
bright jazz music
깊이우선탐색(DFS, Depth-First Search) 본문
깊이우선탐색(DFS, Depth-First Search)
bright jazz music 2024. 11. 3. 11:12
깊이우선 탐색은 그래프나 트리 구조에서 가능한 한 깊이 탐색하다가, 더 이상 탐색할 수 없을 때 다른 경로로 돌아가서 탐색을 계속하는 알고리즘이다.
DFS의 주요 특징:
- 한 방향으로 끝까지 탐색한 후 다음 경로를 탐색한다.
- 재귀 또는 스택을 사용하여 구현할 수 있다.
- 시간 복잡도는 O(V + E)입니다. (V: 정점 수, E: 간선 수)
DFS의 활용 사례:
- 미로 찾기
- 위상 정렬
- 연결 요소 찾기
- 순환 감지
- 경로 찾기
실제로 사용할 때는 방문한 노드를 표시하는 것이 중요하며, 무한 루프를 방지하기 위해 visited 세트를 사용 한다.
// 인접 리스트를 사용한 그래프 구현
const graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
};
/*
재귀(Recursive) 방식
함수가 자기 자신을 호출하는 방식
코드가 더 간단하고 이해하기 쉬움
실제로는 내부적으로 콜 스택을 사용
깊이가 매우 깊은 경우 스택 오버플로우 발생 가능
*/
function dfsRecursive(graph, startNode) {
const visited = new Set();
function dfs(node) {
// 현재 노드를 방문 처리
visited.add(node);
console.log(node); // 방문한 노드 출력
// 현재 노드의 이웃 노드들을 탐색
for (const neighbor of graph[node]) {
if (!visited.has(neighbor)) {
dfs(neighbor);
}
}
}
dfs(startNode);
}
/*
스택(Stack) 방식
명시적으로 스택 자료구조를 사용
메모리를 더 효율적으로 관리 가능
스택 오버플로우 위험이 없음
코드가 조금 더 복잡할 수 있음
*/
function dfsIterative(graph, startNode) {
const visited = new Set();
const stack = [startNode];
while (stack.length > 0) {
const node = stack.pop();
if (!visited.has(node)) {
visited.add(node);
console.log(node); // 방문한 노드 출력
// 이웃 노드들을 스택에 추가
for (const neighbor of graph[node]) {
if (!visited.has(neighbor)) {
stack.push(neighbor);
}
}
}
}
}
// 사용 예시
console.log("재귀적 DFS:");
dfsRecursive(graph, 'A');
console.log("\n반복적 DFS:");
dfsIterative(graph, 'A');
재귀적 방법도 내부적으로는 콜스택을 사용한다. 그러나 아래와 같은 이유로 명시적인 스택 사용 방식을 사용이 일반적이다.
- 메모리 제어의 용이성
- 재귀의 경우 콜스택 크기는 브라우저나 런타임 환경에 따라 제한됨
- JavaScript의 경우 대부분 10,000회 정도의 재귀 호출 제한이 있음
- 스택 오버플로우 방지
- 현재 함수의 상태가 콜스택에 저장됨
- 지역 변수, 매개변수, 반환 주소 등이 메모리를 차지
- 노드가 많아질수록 콜스택이 계속 쌓임
- 결국 브라우저나 런타임의 콜스택 크기 제한에 도달
- 디버깅 용이성
- 명시적 스택을 사용하면 현재 처리 중인 노드들의 상태를 더 쉽게 확인 가능
- 중간에 처리를 중단하거나 재개하기도 용이함
- 메모리 사용량 예측 용이
- 스택 크기를 직접 제어할 수 있어 메모리 사용량 예측이 가능
- 필요한 경우 스택 크기를 제한할 수도 있음
-------------------
선형탐색과 이진탐색은 제약이 있다. 일반적인 배열 형태가 아닌 데이터 형태에 대해서는 탐색이 쉽지 않다.
깊이 우선 탐색(DFS)은 배열로 나타내기 어려운 데이터 형태를 그래프나 트리 형태로 만들어 최적의 해를 찾아내는 데 도움을 준다.
1. 스택
DFS는 스택 구조를 사용한다. 스택은 계속해서 쌓이는 형태를 의미한다. 스택은 후입선출(Last-In, First-Out)하는 데이터 구조이며, 가장 마지막에 추가된 데이터가 가장 먼저 삭제될 수 있다. 가장 처음에 삽입한(push)한 데이터는 나머지 모든 데이터를 삭제한 후에 마지막에 삭제(pop)할 수 있다.
스택은 아래의 연산을 지원한다.
- push: 스택에 데이터를 삽입한다. 스택의 최상단에 추가된다.
- pop: 스택에 데이터를 삭제한다. 스택의 최상단 데이터가 삭제된다.
- peek(or Top): 스택에 맨 위에 데이터를 조회한다.
- isEmpty: 스택이 비어있는지 확인한다. Boolean을 반환한다.
스택은 배열과 유사하지만 배열과 달리 데이터의 입력과 삭제 방식에 제약을 두어 성능상에 이점이 생긴다.
2. 그래프
DFS가 강점을 가지는 두 번째 데이터 타입은 그래프이다.
그래프는 원소 사이에 연결된 형태가 존재할 때 관계를 표현할 수 있는 자료구조이다.
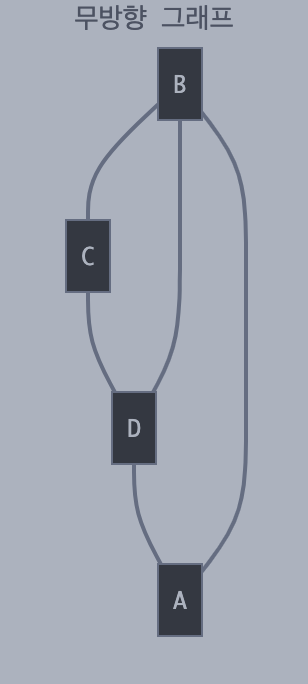
무방향 그래프:
- 노드 간의 연결에 방향이 없다
- 양방향으로 이동이 가능하다
- A-B는 B-A와 동일하다
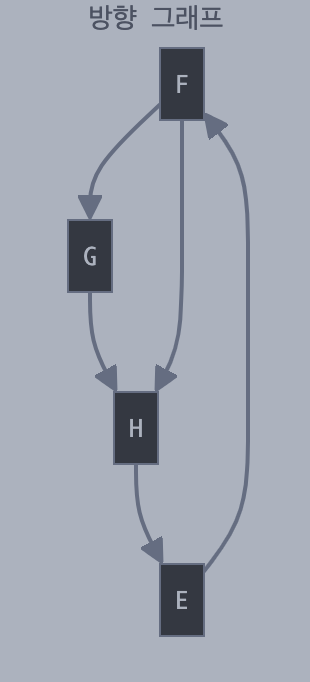
방향 그래프:
- 노드 간의 연결에 방향이 있다
- 화살표 방향으로만 이동이 가능하다
- E→F는 F→E와 다르다
그래프와 트리 자료구조 모두 원소가 노들르 통해 연결돼 있다.
정리하자면, 깊이 우선 탐색(DFS)는 노드 형태의 자료구조를 스택을 사용해 탐색하는 알고리즘이라고 할 수 있다.
예시) 서울에서 부산 가는 방법
- 서울에서 인접한 고양시로 방문 ->
- 고양시에 인접한 다른 시가 있을 경우 방문 ->
- 고양시에 인접한 다른 시가 없는 경우 부산으로의 이동이 불가능하므로, 서울시에서 인접한 다른 시로 방문
===> 이와 같은 방식으로, 더 깊게 탐색이 가능하면 깊게 탐색하는 방식
방문 -> 인접한 지역 존재여부 체크 -> 있으면 방문 후 다시 인접한 지역 체크 -> 없다면 마지막에 만난 분기로 돌아감.
예제1 ) 재귀 방식 사용
// 그래프 데이터를 생성하는 클래스
class SeoulGraph {
constructor() {
this.adjList = new Map(); // 1. 인접한 지역을 저장
}
// 각 지역(정점)을 추가하는 메서드. 즉, 노드 추가 메서드
addVertex(vertex) {
if (!this.adjList.has(vertex)) {
this.adjList.set(vertex, []); // 파라미터명을 key로, 빈 배열을 value로 집어 넣는다.
}
}
// 간선을 추가하는 메서드
addEdge(vertex1, vertex2) {
this.adjList.get(vertex1).push(vertex2); // 키로 밸류(배열)에 상대명을 키로 넣는다.
this.adjList.get(vertex2).push(vertex1);
}
// DFS를 수행하는 메서드
dfs(startVertex) {
const visited = new Set(); //방문한 지역이 저장되는 Set타입 데이터
// 재귀적 dfs
const dfsRecursive = (vertex) => {
visited.add(vertex); // 집합에 넣기
console.log(vertex) // 출력
const neighbors = this.adjList.get(vertex);
for(const neighbor of neighbors) {
if(!visited.has(neighbor)) { // 방문한 집합에 존재하는 않는다면
dfsRecursive(neighbor) // 거기서 다시 dfs시작
}
}
};
dfsRecursive(startVertex);
}
}
// 사용처
const graph = new SeoulGraph(); // 2. 클래스 생성
// 노드 추가
graph.addVertex('강남구');
graph.addVertex('강동구');
graph.addVertex('강북구');
graph.addVertex('서초구');
graph.addVertex('용산구');
graph.addVertex('성동구');
graph.addVertex('광진구');
graph.addVertex('송파구');
// 간선 연결
graph.addEdge('강남구', '서초구')
graph.addEdge('강남구', '용산구')
graph.addEdge('강남구', '성동구')
graph.addEdge('강남구', '광진구')
graph.addEdge('강남구', '송파구')
// 강남구와 간접 연결
graph.addEdge('강동구', '광진구')
graph.addEdge('강동구', '송파구')
// 3. dfs 실행
graph.dfs('강남구');
/*
강남구
서초구
용산구
성동구
광진구
강동구
송파구
-----------
: 깊이우선탐색을 통해 강남구에서 시작해 모든 구를 방문한 순서대로 콘솔에 출력한다.
광진구에 도착했을 때 그 neighbor를 탐색하기 시작하면서 강동구가 먼저 출력됨.(dfs)
이 과정에서 for 문에서 대기(waiting)상태가 되고, 아래로 내려가지 않기 때문에 송파구가 출력되지 않음.
강동구에서 이웃을 찾기 시작하면서 송파구가 출력됨.
// 강남구의 인접 리스트
adjList.get('강남구') = ['서초구', '용산구', '성동구', '광진구', '송파구']
// 광진구의 인접 리스트
adjList.get('광진구') = ['강남구', '강동구']
// 강동구의 인접 리스트
adjList.get('강동구') = ['광진구', '송파구']
// 송파구의 인접 리스트
adjList.get('송파구') = ['강남구', '강동구']
/* 실행 순서
1. 강남구 방문
2. → 인접 리스트 첫번째: 서초구 방문
3. → 인접 리스트 두번째: 용산구 방문
4. → 인접 리스트 세번째: 성동구 방문
5. → 인접 리스트 네번째: 광진구 방문
5-1. 광진구의 인접 리스트 탐색 시작
5-2. 강남구는 이미 방문했으므로 스킵
5-3. 강동구 방문
- 강동구의 인접 리스트 탐색
- 광진구는 이미 방문했으므로 스킵
- 송파구 방문
6. → 인접 리스트 다섯번째: 송파구는 이미 방문했으므로 스킵됨
*/
예제2) 재귀 방식 사용
/*
미로 탈출
미로에서 출구까지 도달하는 경로를 DFS를 이용해서 찾기.
미로는 2차원 배열로 표현되며, 0은 이동 가능 경로, 1은 벽, 'S'는 시작점, 'E'는 출구
상하좌우로만 이동 가능
*/
let maze = [
['S', 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 1],
[0, 0, 0, 0, 'E'],
[1, 1, 1, 0, 1]
];
function dfs(maze, position = [0, 0], path = []) {
let [x, y] = position;
if( maze[x][y] === 'E') {
return [...path, position];
}
let directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for( let [dx, dy] of directions) {
let newX = x + dx;
let newY = y + dy;
if(newX >= 0 && newX < maze.length
&& newY >= 0 && newY < maze[0].length
&& (maze[newX][newY] === 0 || maze[newX][newY] === 'E')) {
maze[x][y] = 1; //방문한 곳 표시
// 재귀 호출
let result = dfs(maze, [newX, newY], [...path, position]);
if(result) {
return result;
}
}
}
return null;
}
console.log(dfs(maze));
/*
[
[ 0, 0 ], [ 0, 1 ],
[ 1, 1 ], [ 1, 0 ],
[ 2, 0 ], [ 3, 0 ],
[ 3, 1 ], [ 3, 2 ],
[ 3, 3 ], [ 3, 4 ]
]
-----
: 시작점부터 끝점까지의 경로가 위처럼 나오는 것이다.
도표화하면 아래와 같다.
[S→*→1→0→0]
[*→*→0→0→0]
[*→1→1→1→1]
[*→*→*→*→E]
[1→1→1→0→1]
*/
예제3) 재귀 방식 사용
/*
지도에서 섬의 개수를 파악하기
2차원 배열을 하나의 지도로 생각하고 땅과 바다를 의미하는 경우를 고려한다.
map이라는 2차원 배열은 지형을 표현한다.
땅은 1로 표시되며 주변 상하좌우로 1로 연결돼 있을 때 섬이 된다.
0은 바다를 나타낸다.
대각선으로 연결된 1은 연결된 것으로 판단하지 않는다.
*/
let map = [
[1, 1, 0, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 0],
]
function dfs(grid, i, j) {
if( i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] === 0 ) {
// i(=x)가 0보다 작거나, j(=y)가 0보다 작거나, 경계를 벗어나거나 바다를 만났을 때는 return
return;
}
grid[i][j] = 0 // 방문한 곳을 표시. 별도의 visited배열을 사용하지 않고 해당 지점을 바다로 만들어 버림으로써 재방문 X
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
function countIslands(grid) {
let count = 0;
// 배열의 길이만큼 순회
for(let i = 0; i < grid.length; i++) {
for(let j = 0; j < grid[0].length; j++) {
// 만약 해당 지점이 섬이라면 dfs재귀호출
if(grid[i][j] === 1) {
dfs(grid, i, j);
count++;
}
}
}
return count;
}
console.log(countIslands(map))
// 3
예제4) 재귀 방식 사용
/*
네트워크 연결 확인
사용자들의 네트워크 연결 확인을 위한 로직 작성
사용자들의 관계는 2차원 배열로 주어지고, 각 배열의 요소는 연결된 두 사용자의 ID를 의미한다.
총 네트워크가 몇 개인지 알아내는 알고리즘 작성할 것
*/
function dfs(node, graph, visited) {
// 현재 노드를 방문 처리
visited[node] = true;
// 현재 노드와 연결된 모든 노드들을 탐색
for(let nextNode of graph[node]) {
// 아직 방문하지 않은 인접 노드가 있다면 해당 노드로 DFS 수행
if (!visited[nextNode]) {
dfs(nextNode, graph, visited)
}
}
}
function countNetworks(connections) {
let graph = {}; // 인접 리스트로 구현할 그래프 객체
let visited = {}; // 노드 방문 여부를 저장할 객체
let count = 0; // 네트워크 개수를 카운트
// 무방향 그래프 생성
for (let [node1, node2] of connections) {
// 처음 보는 노드라면 빈 배열로 초기화
if(!graph[node1]) graph[node1] = [];
if(!graph[node2]) graph[node2] = [];
// 양방향 연결 추가 (무방향 그래프이므로 양쪽에 추가)
graph[node1].push(node2);
graph[node2].push(node1);
// 모든 노드를 미방문 상태로 초기화
visited[node1] = false;
visited[node2] = false;
}
// 모든 노드에 대해 미방문 노드를 시작점으로 DFS 수행
for(let node in graph) {
// 아직 방문하지 않은 노드를 발견하면
// 새로운 네트워크의 시작점이므로 DFS 수행하고 카운트 증가
if(!visited[node]) {
dfs(node, graph, visited);
count++;
}
}
return count;
}
let connections = [
[1, 2],
[1, 3],
[2, 3],
[3, 4],
[5, 6],
]
console.log(countNetworks(connections))
// 결과: 2 (1-2-3-4와 5-6, 두 개의 독립된 네트워크가 존재)'Algorithm&Data structure > JS alg.' 카테고리의 다른 글
| 최소신장트리(Minimum Spanning Tree, MST) + (프림, 크루스칼 알고리즘) (0) | 2024.11.05 |
|---|---|
| 너비우선탐색(Breadth-First Search, BFS) (0) | 2024.11.04 |
| 이진탐색(Binary Search) (0) | 2024.11.01 |
| 선형탐색(Linear Search)과 Array.prototype.find() (0) | 2024.10.31 |
| Array.prototype.sort() 메서드 (0) | 2024.10.30 |

