Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 리눅스
- 서버설정
- baeldung
- 페이징
- 스프링부트핵심가이드
- 처음 만나는 AI수학 with Python
- resttemplate
- 선형대수
- 목록처리
- /etc/network/interfaces
- 티스토리 쿠키 삭제
- 네트워크 설정
- 데비안
- 코드로배우는스프링부트웹프로젝트
- 자료구조와함께배우는알고리즘입문
- 코드로배우는스프링웹프로젝트
- d
- 처음 만나는 AI 수학 with Python
- 자바편
- iterator
- 이터레이터
- Kernighan의 C언어 프로그래밍
- GIT
- 구멍가게코딩단
- network configuration
- 친절한SQL튜닝
- 자료구조와 함께 배우는 알고리즘 입문
- 알파회계
- 스프링 시큐리티
- ㅒ
Archives
- Today
- Total
bright jazz music
이진 탐색 트리(Binary Search Tree, BST)와 BFS, DFS 본문
Algorithm&Data structure/Data structure(JS)
이진 탐색 트리(Binary Search Tree, BST)와 BFS, DFS
bright jazz music 2024. 12. 11. 21:28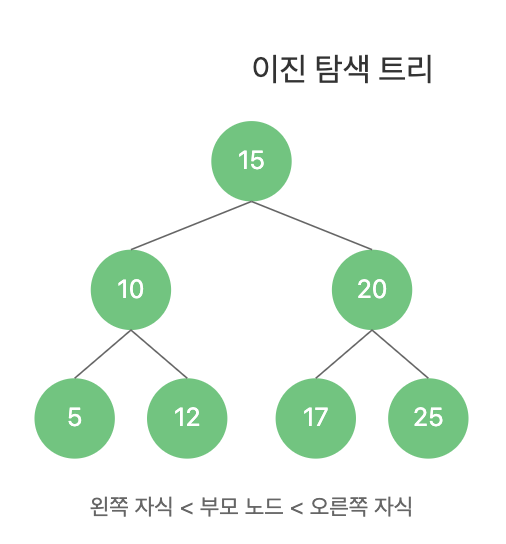
1. 이진 탐색 트리(Binary Search Tree)
이진 탐색 트리는 각 노드가 최대 두 개의 자식을 가지며, 왼쪽 자식은 현재 노드보다 작은 값, 오른쪽 자식은 큰 값을 가지는 특별한 형태의 이진 트리이다.
필수 구현 메서드:
- insert(value) - 새로운 값을 적절한 위치에 삽입
- find(value) - 특정 값을 찾아서 반환
- remove(value) - 특정 값을 가진 노드를 삭제
- getMin() - 최솟값(가장 왼쪽 노드) 반환
- getMax() - 최댓값(가장 오른쪽 노드) 반환
주요 구현 포인트:
1. 삽입 시 순서 결정:
if (value < node.value) {
if (!node.left) node.left = new Node(value);
else insert(node.left, value);
} else {
if (!node.right) node.right = new Node(value);
else insert(node.right, value);
}
2. 삭제 시 3가지 경우 처리:
- 리프 노드: 직접 삭제
- 하나의 자식: 자식을 현재 위치로 승격
- 두 개의 자식: 중위 후속자로 대체
3. 균형 관리:
- 트리가 한쪽으로 치우치지 않도록 관리
- 필요시 회전 연산 구현 (AVL, Red-Black 트리)
시간 복잡도:
- 평균 케이스: O(log n) - 검색, 삽입, 삭제
- 최악 케이스: O(n) - 트리가 한쪽으로 치우친 경우
활용 사례:
- 데이터베이스 인덱싱
- 파일 시스템 구조
- 우선순위 큐 구현
- 검색 알고리즘 최적화
이진 탐색 트리는 효율적인 검색과 정렬된 데이터 유지가 필요한 경우에 유용하다.
데이터의 삽입/삭제가 빈번한 동적 데이터 집합을 다루는 경우 이진 탐색 트리를 사용하는 경우가 많다.
구현
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
if( this.root === null ) {
this.root = newNode;
return this;
}
// 만약 루트가 있는 경우 최초에는 루트이다.
let current = this.root;
while(true) {
// 이미 존재해서 인서트가 불가능하기 때문에
if(value === current.value) return false;
if(value < current.value) {
if(current.left === null) {
current.left = newNode;
return this;
}
// 한 층 아래로 내려가기
current = current.left;
} else {
if(current.right === null) {
current.right = newNode;
return this;
}
// 한 층 아래로 내려가기
current = current.right;
}
}
}
find(value) {
if(this.root === null) return false;
let current = this.root;
let found = false;
while(current && !found) {
if(value < current.value) {
current = current.left;
} else if(value > current.value) {
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contain(value) {
if(this.root === null) return false;
let current = this.root;
while(current) {
if(value < current.value) {
current = current.left;
} else if(value > current.value) {
current = current.right;
} else {
return true;
}
}
return false;
}
getMin() {
if(!this.root) return null;
let current = this.root;
while(current.left) {
current = current.left;
}
return current.value;
}
getMax() {
if(!this.root) return null;
let current = this.root;
while(current.right) {
current = current.right;
}
return current.value;
}
remove(value) {
if(!this.root) return false;
let current = this.root;
let parent = null;
let isLeftChild = true;
// 삭제할 노드 찾기 & 그 노드의 부모 추적하기(노드 삭제 시 부모의 포인터 수정 위해)
// 현재 노드가 존재하고, 그 값이 제거하려는 값과 다른 경우
// 현재 노드가 존재하지 않거나, (제거하려는 값이 없는 경우)
// 값이 같으면 순회 중지(타겟 노드 찾음)
while(current && current.value !== value) {
parent = current;
if(value < current.value) {
isLeftChild = true;
current = current.left;
} else {
isLeftChild = false;
current = current.right;
}
}
// 값이 없는 경우 false
if(!current) return false;
// 이 부분부터는 찾은 current 노드를 제거한 뒤 이어붙이는 목적 때문에 존재하는 코드이다.
// Case 1: 리프 노드인 경우 (자식이 없는 경우)
// 부모 노드의 left와 right를 null로 정해버리면 끝. 제거된 노드가 말단 노드였기 때문에.
if(!current.left && !current.right) {
if(current === this.root) {
this.root = null;
} else if(isLeftChild) {
parent.left = null;
} else {
parent.right = null;
}
}
// Case 2: 하나의 자식만 있는 경우
else if(!current.right) {
// 왼쪽 자식만 있는 경우
// 즉, 제거한 노드가 루트 노드인 경우, 왼쪽 자식이 루트 노드가 됨.
if(current === this.root) {
this.root = current.left;
} else if(isLeftChild) {
// 제거한 노드가 루트 노드가 아니고 그 노드가 왼쪽 자식이 있는 경우
// 왼쪽 자식 노드가 부모노드가 됨(오른쪽은 부모보다 크므로)
parent.left = current.left;
} else {
// 제거한 노드는 왼쪽 자식만 있지만,
// 제거한 노드 자체는 부모 노드의 오른쪽 자식이었으므로, 거기에 손자를 붙임
parent.right = current.left;
}
}
else if(!current.left) {
// 오른쪽 자식만 있는 경우
if(current === this.root) {
this.root = current.right;
} else if(isLeftChild) {
parent.left = current.right;
} else {
parent.right = current.right;
}
}
// Case 3: 두 개의 자식이 있는 경우
else {
// 후계자 찾기(오른쪽 서브트리의 최솟값)
let successor = this.getSuccessor(current);
if(current === this.root) {
this.root = successor;
} else if(isLeftChild) {
parent.left = successor;
} else {
parent.right = successor;
}
// 위 코드에서 오른쪽 서브트리는 연결됐지만 왼쪽은 연결 안 됐으므로
// 연결해준다.
successor.left = current.left;
}
return true;
}
// remove 헬퍼 메서드: 후계자(successor) 찾기
getSuccessor(node) {
// 후계자의 부모는 떼어낼 때 필요
let successorParent = node;
let successor = node;
// 이진 서브트리에서 부모 노드는 왼쪽 자식보다는 커야하기 때문에 최초에 오른쪽에서 찾는 것이다.
let current = node.right;
// 후계자 찾기(오른쪽 서브트리에서 가장 작은 값)
while (current) {
successorParent = successor;
successor = current;
// 왼쪽이 없을 때까지 찾는 과정
// 왼쪽은 부모보다 작으므로 왼쪽에서 찾는 것이다.
// 오른쪽 자식의 부모는 자식보다 작으므로, 자손이 조상이 되어야 하는 것이다
current = current.left;
}
// 후계자가 삭제할 노드의 직계 자식이 아닌 경우
if(successor !== node.right) {
// 부모 노드의 왼쪽(자기가 있던 자리)에 오른쪽 손자를 붙임
successorParent.left = successor.right;
// 제거 노드의 오른쪽 자식이자 원래 후계자의 조상이었던 노드가
// 후계자 노드가 제거 노드의 자리에 오게 됨으로써 후계자 노드의 자식 노드가 됨
successor.right = node.right;
}
return successor;
}
// 너비 우선 탐색 (BFS - Breadth First Search)
BFS() {
let node = this.root;
// 순회하며 수집한 값들의 배열
const visited = [];
// 미방문한 노드들을 순서대로 저장하는 대기열. FIFO
const queue = [];
queue.push(node);
while(queue.length) {
node = queue.shift(); // 큐에서 꺼내서 방문한 배열에 넣기
visited.push(node.value); // data.push(node)로 하면 객체가 저장됨
// 왼쪽 자식이 있으면 큐에 추가(방금 노드를 꺼낸 큐에 추가되는 것이다)
if(node.left) queue.push(node.left);
// 오른쪽 자식이 있으면 큐에 추가(방금 노드를 꺼낸 큐에 추가되는 것이다)
if(node.right) queue.push(node.right);
}
// 방문한 순서대로 배열에 넣고 반환
return visited;
}
// 전위 순회(부모가 우선 기록되고 그 다음 왼쪽, 오른쪽 순으로 처리 => 노드 -> 왼 -> 오)
DFSPreOrder(current = this.root) {
let visited = [];
// 순회 함수 작성
function traverse(node) {
// 먼저 넣기
visited.push(node.value);
// 왼쪽부터 재귀(재귀가 끝나면 자연스럽게 상위 호출부로 돌아온다)
// 따라서 더이상 왼쪽이 없으면 부모로 올라와서 오른쪽이 있는지 살피게 된다
if(node.left) traverse(node.left);
// 왼쪽이 끝나면 오른쪽 재귀
if(node.right) traverse(node.right);
}
traverse(current);
return visited;
}
// 후위 순회(자식들이 먼저 기록되고, 부모는 마지막에 처리 => 왼쪽 → 오른쪽 → 노드)
DFSPostOrder(current = this.root) {
let visited = [];
function traverse(node) {
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
// 나중에 넣어줌
visited.push(node.value);
}
traverse(current);
return visited;
}
// 중위 순회(왼쪽 자식부터 기록되고, 왼쪽이 끝나면 해당 노드 기록,
// 그리고 오른쪽 자식 기록 => 왼쪽 → 노드 → 오른쪽)
DFSInOrder(current = this.root) {
let visited = [];
function traverse(node) {
// 왼쪽 먼저 기록
if(node.left) traverse(node.left);
visited.push(node.value);
if(node.right) traverse(node.right);
}
traverse(current);
return visited;
}
}---
const bst = new BinarySearchTree();
bst.insert(10);
bst.insert(5);
bst.insert(15);
bst.insert(2);
bst.insert(7);
console.log(bst.getMin()); // 2
console.log(bst.getMax()); // 15
console.log(bst.contains(7)); // true
bst.remove(5);
console.log(bst.contains(5)); // false
2. 이진탐색트리의 BFS 와 DFS 의 예시
각 순회 방식의 특징:
- BFS: 레벨 순서대로 방문하여 같은 깊이의 노드들(형제 노드)을 순차적으로 처리
- DFS 전위: 부모를 먼저 방문한 후 자식들을 방문 (루트 우선)
- DFS 후위: 자식들을 모두 방문한 후 부모를 방문 (리프 노드 우선)
- DFS 중위: 왼쪽 자식, 부모, 오른쪽 자식 순으로 방문 (오름차순 정렬된 결과)
10
/ \
6 15
/ \ / \
3 8 13 20
트리 생성
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(13);
tree.insert(20);
BFS 예시
console.log(tree.BFS());
// 결과: [10, 6, 15, 3, 8, 13, 20]
/*
순회 과정:
레벨 0: 10
레벨 1: 6, 15
레벨 2: 3, 8, 13, 20
*/
DFS 예시
1) 전위 순회(pre-order)
console.log(tree.DFSPreOrder());
// 결과: [10, 6, 3, 8, 15, 13, 20]
/*
순회 과정:
루트(10) 방문
왼쪽으로 가서 6 방문
3 방문
8 방문
오른쪽으로 가서 15 방문
13 방문
20 방문
*/
2) 후위 순회(post-order)
console.log(tree.DFSPostOrder());
// 결과: [3, 8, 6, 13, 20, 15, 10]
/*
순회 과정:
가장 왼쪽 리프인 3 방문
8 방문
부모인 6 방문
13 방문
20 방문
15 방문
마지막으로 루트인 10 방문
*/
3) 중위 순회(in-order)
console.log(tree.DFSInOrder());
// 결과: [3, 6, 8, 10, 13, 15, 20]
/*
순회 과정:
가장 왼쪽 3 방문
부모인 6 방문
8 방문
루트인 10 방문
13 방문
15 방문
20 방문
*/
3. 이진탐색트리에 대 해 BFS와 DFS를 선택하는 기준
BFS와 DFS의 선택은 문제의 성격과 트리의 구조에 따라 달라진다.
BFS(너비 우선 탐색)이 유리한 경우:
- 트리가 깊고 좁은 경우 (메모리 관점)
- 각 레벨에서 처리할 노드가 적어 큐의 크기가 작게 유지됨
- 한 번에 저장되는 노드의 수가 적음
- 최단 경로 찾기
- 출발지에서 가장 가까운 노드부터 탐색
- 예: 최단 거리, 최소 이동 횟수 문제
- 레벨 단위의 처리가 필요한 경우
- 트리의 각 층을 순서대로 처리해야 할 때
- 예: 조직도에서 각 직급별 처리
DFS(깊이 우선 탐색)이 유리한 경우:
- 트리가 넓은 경우 (메모리 관점)
- 형제 노드가 많은 경우
- 현재 경로의 노드만 스택에 저장하므로 메모리 효율적
- 경로 탐색이 필요한 경우
- 특정 경로의 존재 여부 확인
- 예: 미로 찾기, 경로 존재 확인
- 트리의 모든 노드를 방문해야 할 때
- 예: 파일 시스템 탐색, 모든 하위 디렉토리 검색
각 DFS 순회 방식의 활용:
- 전위 순회(Pre-order): 노드 → 왼쪽 → 오른쪽
- 트리 구조 복사
- 디렉토리 구조 출력
- 중위 순회(In-order): 왼쪽 → 노드 → 오른쪽
- 이진 검색 트리에서 정렬된 순서 얻기
- 수식 트리에서 중위 표기식 생성
- 후위 순회(Post-order): 왼쪽 → 오른쪽 → 노드
- 트리 삭제 (자식부터 삭제)
- 디렉토리 용량 계산 (하위 항목부터 계산)
넓은 트리의 경우:
A
/ / | \ \
B C D E F
BFS: 큐에 [B,C,D,E,F] 모두 저장 → 많은 메모리 필요
DFS: 한 번에 한 경로만 저장 [A,B] → 메모리 효율적
깊은 트리의 경우:
A
|
B
|
C
|
D
BFS: 큐에 한 번에 하나의 노드만 저장 → 메모리 효율적
DFS: 스택에 전체 경로 [A,B,C,D] 저장 → 더 많은 메모리 사용'Algorithm&Data structure > Data structure(JS)' 카테고리의 다른 글
| 우선순위 큐(Priority Queue) (0) | 2024.12.12 |
|---|---|
| 이진 힙(Binary Heaps)과 최대힙, 최소힙 (0) | 2024.12.12 |
| 트리 (Tree, Data Tree) (1) | 2024.12.11 |
| 스택 (Stack)과 큐 (Queue) (0) | 2024.12.09 |
| 이중 연결리스트 (Doubly Linked List) (0) | 2024.12.08 |
Comments


