Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 서버설정
- 알파회계
- 자바편
- 친절한SQL튜닝
- 처음 만나는 AI수학 with Python
- GIT
- 구멍가게코딩단
- 목록처리
- 자료구조와함께배우는알고리즘입문
- resttemplate
- 리눅스
- network configuration
- 페이징
- Kernighan의 C언어 프로그래밍
- /etc/network/interfaces
- 티스토리 쿠키 삭제
- 코드로배우는스프링웹프로젝트
- 처음 만나는 AI 수학 with Python
- 코드로배우는스프링부트웹프로젝트
- d
- 데비안
- 자료구조와 함께 배우는 알고리즘 입문
- baeldung
- 스프링 시큐리티
- iterator
- 네트워크 설정
- ㅒ
- 스프링부트핵심가이드
- 선형대수
- 이터레이터
Archives
- Today
- Total
bright jazz music
선형대수: 14. 고윳값과 고유벡터, 그리고 고유 방정식 (2) 본문
고윳값과 고유벡터의 계산
- 행렬을 고유방정식에 대입하여 고윳값을 먼저 구한다.
- 구한 각각의 고윳값에 대한 고유벡터를 구한다.
1. 고윳값의 계산
- 다음 행렬 A의 고윳값을 계산한다.
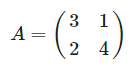
고유방정식 사용 (A를 고유방정식에 대입)
| LaTeX | 수식 |
| $\begin{align} det(A-\lambda{E}) &= 0 \\ \\ det\begin{pmatrix} \begin{pmatrix} 3&1 \\ 2&4 \end{pmatrix} -\lambda \begin{pmatrix} 1&0 \\ 0&1 \end{pmatrix} \end{pmatrix} &= 0 \\ \\ det\begin{pmatrix} 3-\lambda & 1 \\ 2 & 4-\lambda \end{pmatrix} &= 0\\ \\ (3-\lambda)(4-\lambda) -1\times{2} &= 0\\ \\ \lambda^{2} -7\lambda + 10 &= 0 \\ \\ (\lambda - 2)(\lambda - 5) &= 0 \end{align}$ |
 |
- 이 때 고윳값 λ의 값은 2 또는 5가 된다.
고윳값을 구했으니 이제 고유벡터를 구할 차례이다.
2. 고유벡터의 계산
고윳값 λ가 2인 경우와 5인 경우의 두 가지 모두 생각한다.
2-1. λ가 2인 경우
- λ = 2인 경우, 벡터 x가 아래와 같다고 가정하자.
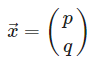
- 아래의 식에 고윳값 λ와 벡터 x를 대입하자.

- 아래와 같이 전개 가능하다.
| LaTeX | 수식 |
| $\begin{align} (A-2E) \begin{pmatrix}p \\ q \end{pmatrix} &= \vec{0} \\ \\ \begin{pmatrix} 3-2 & 1 \\ 2 & 4-2 \end{pmatrix} \begin{pmatrix}p \\ q \end{pmatrix} &= 0 \\ \\ \begin{pmatrix}1 & 1 \\ 2 & 2 \end{pmatrix}\begin{pmatrix}p \\ q \end{pmatrix}&= \vec{0} \\ \\ \begin{pmatrix}p+q \\ 2p+2q \end{pmatrix} &= \vec{0} \end{align}$ |
 |
- 이 때 p + q = 0 이다.
- 이 조건을 만족하는 다음과 같은 벡터가 λ = 2인 경우, A의 고유벡터가 된다.
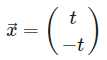
- t는 임의의 실수이다.
2-2. λ가 5인 경우
- λ = 5인 경우, 벡터 x가 아래와 같다고 가정하자.
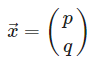
- 아래의 식에 고윳값 λ와 벡터 x를 대입하자.

- 아래와 같이 전개 가능하다.
| LaTeX | 수식 |
| $\begin{align} (A-5E) \begin{pmatrix}p \\ q \end{pmatrix} &= \vec{0} \\ \\ \begin{pmatrix} 3-5 & 1 \\ 2 & 4-5 \end{pmatrix} \begin{pmatrix}p \\ q \end{pmatrix} &= 0 \\ \\ \begin{pmatrix}-2 & 1 \\ 2 & -2 \end{pmatrix}\begin{pmatrix}p \\ q \end{pmatrix}&= \vec{0} \\ \\ \begin{pmatrix} -2p+q \\ 2p-q \end{pmatrix} &= \vec{0} \end{align}$ |
 |
이 때, 2p - q = 0이다.
이 조건을 만족하는 다음과 같은 벡터가 λ = 5인 경우, A의 고유벡터가 된다. t는 임의의 실수이다.
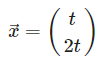
파이썬에서의 고윳값과 고유벡터 계산
고윳값과 고유벡터는 NumPy의 linalg.eig() 함수를 사용해 구할 수 있다.
import numpy as np
a = np.array([[3, 1],
[2, 4]])
ev = np.linalg.eig(a) #고윳값과 고유벡터를 동시에 구한다.
print(ev[0]) # 첫 요소는 고윳값
print()
print(ev[1]) # 두 번째 요소가 고유벡터
print()
#norm 구하기
print(np.linalg.norm(np.array([-0.70710678, 0.70710678]))) #L2 norm
print(np.linalg.norm(np.array([-0.4472136, -0.89442719]))) #L2 norm
# print(np.linalg.norm(a, 1)) #L1 norm
# [2. 5.]
#
# [[-0.70710678 -0.4472136 ]
# [ 0.70710678 -0.89442719]]
#
# 0.9999999983219684
# 1.000000001118128
#lin.alg() 함수는 두 개의 배열이 들어있는 중복 리스트를 반환한다.
# 첫 번째 배열이 고유값을 가지고 있다.
# 두 번째 배열이 고유벡터를 가지고 있다.
#고유벡터는 행렬로 얻을 수 있다.
#행렬의 각 "열"이 고유벡터이다. e.g. [-0.70710678, 0.70710678] or -0.4472136, -0.89442719
#이 경우 각 고유벡터는 L2놈이 1이 된다.
#L2 놈이 1인 벡터를 "단위벡터"라고 한다.
#Numpy의 linalg.eig()함수는 고유벡터를 단위벡터의 형태로 반환한다.
'Math > 선형대수' 카테고리의 다른 글
| 선형대수 : 15. 코사인 유사도(cosine similarity) (0) | 2022.08.03 |
|---|---|
| 선형대수: 14. 고윳값과 고유벡터, 그리고 고유 방정식 (1) (0) | 2022.08.02 |
| 선형대수: 13. 표준기저 (Standard basis) (0) | 2022.08.01 |
| 선형대수: 12. 선형변환(linear transformation) (0) | 2022.07.30 |
| 선형대수: 11. 벡터 그리기 (화살표 그리기) (0) | 2022.07.30 |
Comments




