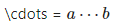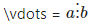Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- d
- 자바편
- iterator
- network configuration
- baeldung
- 구멍가게코딩단
- 페이징
- 스프링 시큐리티
- 목록처리
- 처음 만나는 AI수학 with Python
- 네트워크 설정
- 티스토리 쿠키 삭제
- 알파회계
- 코드로배우는스프링웹프로젝트
- 이터레이터
- 자료구조와함께배우는알고리즘입문
- 자료구조와 함께 배우는 알고리즘 입문
- /etc/network/interfaces
- 선형대수
- 친절한SQL튜닝
- 데비안
- 리눅스
- 처음 만나는 AI 수학 with Python
- GIT
- resttemplate
- 코드로배우는스프링부트웹프로젝트
- 스프링부트핵심가이드
- ㅒ
- 서버설정
- Kernighan의 C언어 프로그래밍
Archives
- Today
- Total
bright jazz music
선형대수 : 2. 스칼라와 벡터 본문
스칼라의 개념
- 스칼라(scarla)는 1, 5, 2, -7 등의 보통의 수치를 의미한다.
- 수식에서의 알파벳 또는 그리스 소문자로 스칼라를 나타내기도 한다.
파이썬에서의 스칼라 구현
a = 1
b = 1.2
c = -0.25
d = 1.2e5 #1.2 * (10의 5제곱 = 120000)
-----
벡터의 개념
- 벡터는 스칼라를 직선 상에 나열한 것이다.
- 알파벳 소문자 위에 화살표를 올린 것으로 벡터를 표현하기도 한다.
가로벡터와 세로벡터
벡터에는 세로로 수치를 나열하는 세로 벡터와 가로로 수치를 나열하는 가로 벡터가 있다.
가로벡터(horizontal vector, row vector)
| 가로 벡터 LaTeX 표기 | 수식 변환 |
| $\vec{a} = (1, 2, 3)$ |
세로벡터(vertical vector, column vector)
| 세로 벡터 LaTeX 표기 | 수식 변환 |
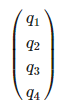
| $\begin{pmatrix}q_1\\q_2\\q_3\\q_4\end{pmatrix}$ 환경에 따라 아래와 같이 사용할 수 있는 경우도 존재 $\begin{pmatrix} q_1\\ q_2\\ q_3\\ q_4 \end{pmatrix}$ |
 |
| $\begin{bmatrix}x_{1} \\ x_{2} \\ \vdots \\ x_{m} \end{bmatrix}$ 환경에 따라 아래와 같이 사용할 수 있는 경우도 존재 $\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{m} \end{bmatrix}$ |
 |
| $\vec{a} = \begin{pmatrix}q_1\\q_2\\q_3\\q_4\end{pmatrix}$ |  |
●\begin{ } 내부의 pmatrix와 bmatrix 의 차이에 주목할 것.
- pmatrix를 사용할 경우 소괄호가 적용된다. (parenthesis matrix로 추정)
- bmatrix 를 사용할 경우 대괄호가 적용된다.(bracket matrix로 추정)
●마지막 수치 뒤에는 \\를 붙이지 않는다.
- q_4와 x_{m} 뒤에는 \\가 붙지 않았다
● end 앞에는 꼭 \를 붙여줄 것.
- 맨 끝 end의 앞에는 꼭 \가 붙어 있어야 한다. 떨어져 있으면 수식으로 변환되지 않는다.
파이썬에서의 벡터 구현(가로)
import numpy as np
a = np.array([1, 2, 3]) #1차원 배열로 벡터를 표현한다
print(a)
b = [-2.4, 0.25, -1.3, 1.8, 0.61]
b_array = np.array(b)
print(b_array)
# [1 2 3]
# [-2.4 0.25 -1.3 1.8 0.61]1차원 배열로 벡터를 표현한다.
---
참고
기본적인 점표시
| 종류 | 의미 | 표기( 뒤 한 칸 띄어줘야 한다) | 수식 |
| \ddots | 대각선 점표시 | \ddots = $a\ddots b$ | |
| \dots | 아래에 점 표시 | \dots = $a\dots b$ | |
| \cdots | 행 중간center에 점 표시 | \cdots = $a\cdots b$ | |
| \vdots | 수직으로 점표시 | \vdots = $a\vdots b$ |
이 외에도 다양한 점 표시가 존재함
'Math > 선형대수' 카테고리의 다른 글
| 선형대수 : 6. 놈 (노름, norm) (0) | 2022.07.24 |
|---|---|
| 선형대수 : 5. 내적(스칼라 곱,dot product, scarla product) (0) | 2022.07.23 |
| 선형대수 : 4. 텐서(Tensor) (0) | 2022.07.22 |
| 선형대수 : 3. 행렬 (0) | 2022.07.22 |
| 선형대수 : 1. 선형대수의 개념 (0) | 2022.07.20 |
Comments